[세상의 변화는 객관적인가 아니면 주관적인가? 역사는 우연으로 랜덤하게만 흘러가는가 아니면 목적을 성취하기 위해 변해가는가? 이에 대한 논쟁은 다양하지만 크게 두 가지 세계관으로 나누어 본다면, 그 하나는 17세기 데카르트로부터 시작되어 19세기 뉴턴의 고전물리학으로 이어지는 기계적 또는 결정론적 세계관입니다. 즉 모든 현상을 자연의 인과관계와 역학적 법칙으로 바라보는 세계관과 20세기에 이에 대한 반발로 출현한 세계관이 아인슈타인의 상대성 원리와 양자물리학을 바탕으로 제시된 주관적 비결정론적 세계관이죠. 현재는 이 둘이 통합된 세계관이 주류인데, 마치 대립되는 것처럼 보이는 두 세계관은 사실 양자역학의 확률적 세계관으로 통합될 수 있는데, 이유는 확율은 미시세계에서는 불확실성이 커지지만 거시세계에서는 확실성이 높아지기 때문이죠. 그런데 필연과 우연이 통합된 세계관이 오일러 공식에 함축되어 있는 듯한데, 이 단순하면서도 함축적이며 시적인 공식은 마치 동양의 우주론의 정수를 함축하고 있는 것 같습니다.]
자연상수 e-자연의 모든 현상은 e로 표현할 수 있다(박문호)
https://www.youtube.com/watch?v=_1xWhTTzgis&t=439s
e는 자연을 대표하는 상수, 자연에 있는 모든 현상은 이 e로써 표현할 수 있다고 생각하시면 되요.
e는 숫자, 2.718281828,,, 순환하지 않는 무한소수인 무리수, 2와 3사이에 위치한 숫자죠, 상수입니다.
이 e에 알수 없는 미지수 x를 지수로 붙이면서 모든 자연과학이 시작되었다 생각합니다.
숫자 3의 지수 x에는 숫자만 들어가는데, e의 지수 x에는 숫자를 포함해 행렬, 복소수 등도 들어간다.
이것을 이해하면 왜 이 e가 자연과학의 모든 것을 통합하는지를 알 수 있는 거예요.
e는 상수죠. 상수는 정해져 있잖아요. 이건 건드릴 수 없잖아요. 붙박이, 불변성이죠.
그럼, x는 뭐죠? 이건 미지수죠. 알수 없다, 정해지지 않았다, 즉 내가 정하면 된다는 가변성이죠.
그럼 이제 뭐든지 할 수 있는 자유가 주어졌다는 거예요.
예를 들면, 5는 상수죠. 상수는 미분해도 바뀌지 않죠. 따라서 5를 미분한 값은 0이죠. (5)' = 0
수학을 하려면 먼저 숫자, 즉 상수에 함축된 정보들을 파악할 줄 알아야 하는데,
일단 5라는 숫자를 보면,
숫자 5는 불변의 상수라는 것을 파악해야 하고,
다음은 이것 앞에 +부호(+5)가 붙었다는 것을 알아야 하고,
세번째 5에 곱하기 1(5*1)을 해도 된다는 거죠. 이게 항등원, 역원 개념이죠.
궁극의 숫자, 진짜 숫자는 1과 0밖에 없습니다. 나머지는 허상입니다.
0은 덧셈에서 항등원, 1은 곱셈에서 항등원, 사칙연산도 궁극적으로 덧셈밖에 없습니다. 빼기는 더하기의 다른 모습이고, 나누기는 곱하기의 변형된 모습인데, 곱하기는 더하기를 반복하는 것이잖아요. 그럼 더하기는 뭐냐? 궁극적으로 더하기는 1,2,3,4,5,6,7,8, 이것은 각각 하나씩을 더해준 건데, 이게 주기율표잖아요.

수학은 한마디로 논리적 동의반복이다.
e의 0승은 1
e의 1승은 e
e의 2승은 e*e
e의 3승은 e*e*e
자연상수 e에 대해 잘 정리된 블러그 클릭
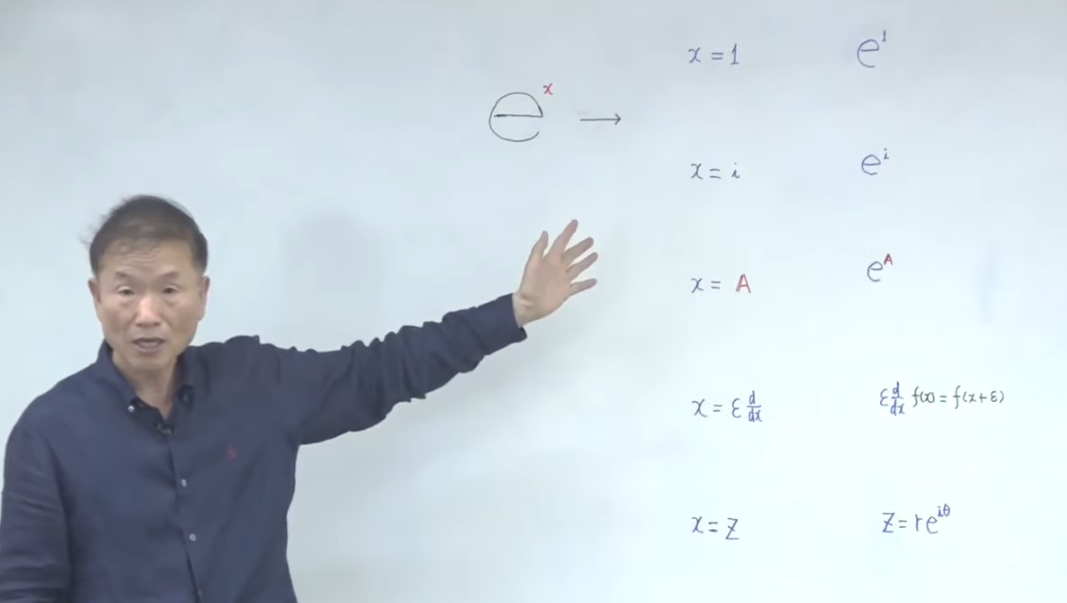
e는 상수(불변값)고, x는 미지수(가변값)인데, x엔 뭐든지 대입이 가능하다고 했죠.
그럼, x에 상수를 집어넣을 수도 있고,
x에 허수 i를 넣을 수도 있고,
x에 행렬 A를 넣을 수도 있고,
x에 미분함수를 넣을 수도 있고,
x에 복소수함수를 넣을 수도 있다.
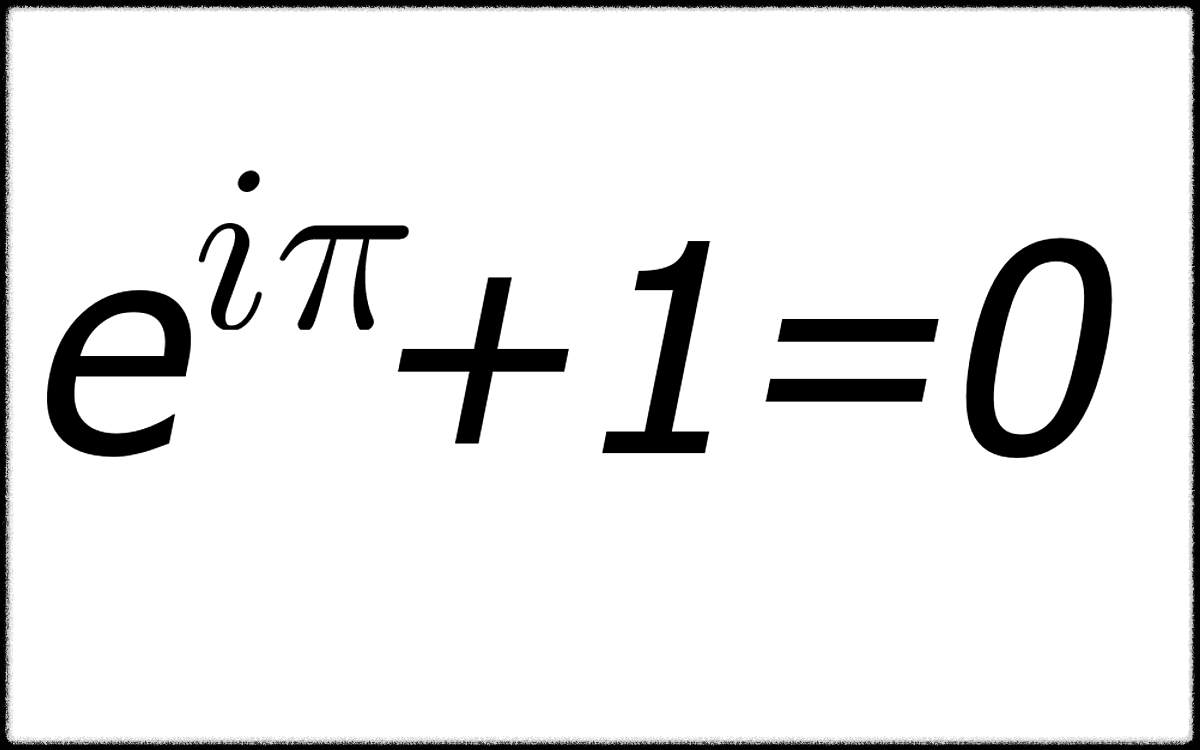
세상에서 가장 아름다운 수학공식이라는 오일러 공식, 여기서 사용된 0과 1, 그리고 허수 i와 자연상수 e, 원주율 π, 이것은 동양우주론에서 사용되는 핵심개념인 0 무극과 1 태극, 그리고 숫자 3으로 수렴되는 자연상수 e와 자연상수 e의 x승값을 -1로 수렴시키는 변수 i π, 그리고 마지막으로 e의 iπ승값이 -1로 수렴되게 하는 cosx+ i sinx 의 삼각함수 그래프, 아래는 오일러 공식을 3D 공간에 나타낸 기하학적 표현 (나선형 회전모형)
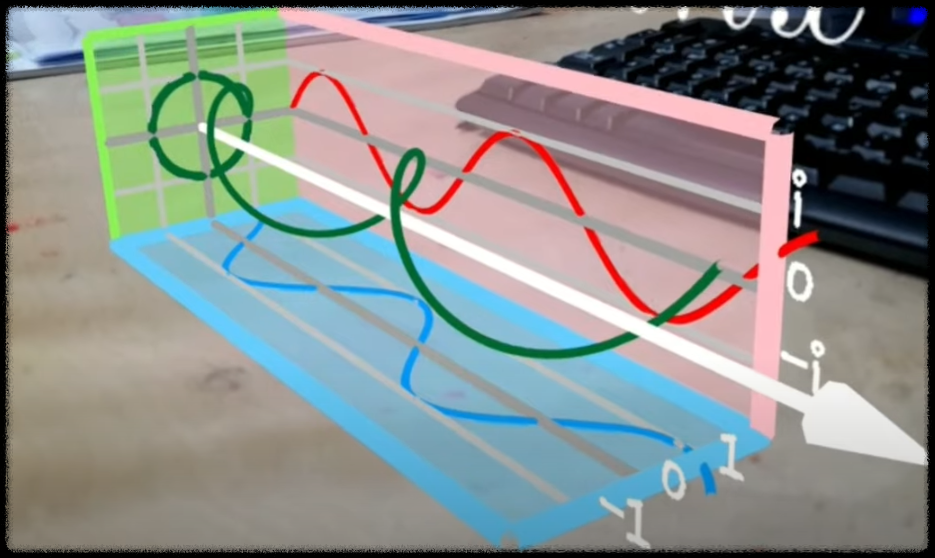
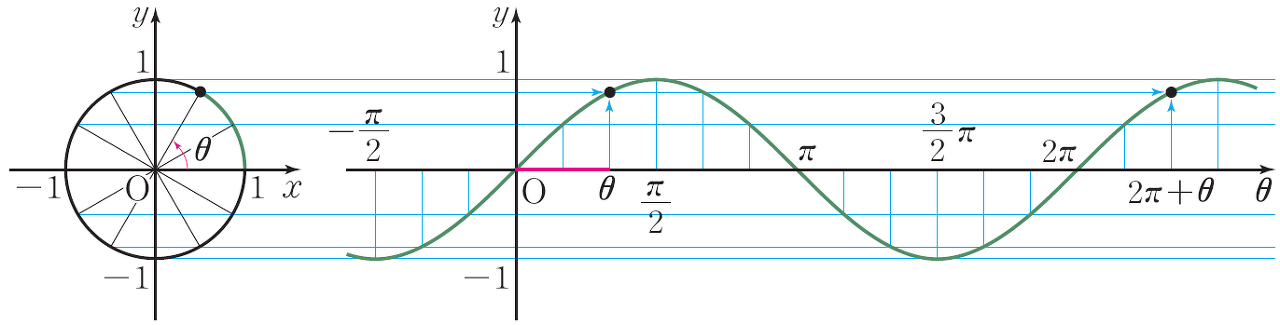
세상에서 가장 아름다운 수식을 이해해보자
https://www.youtube.com/watch?v=xdsGmMI8Vjs
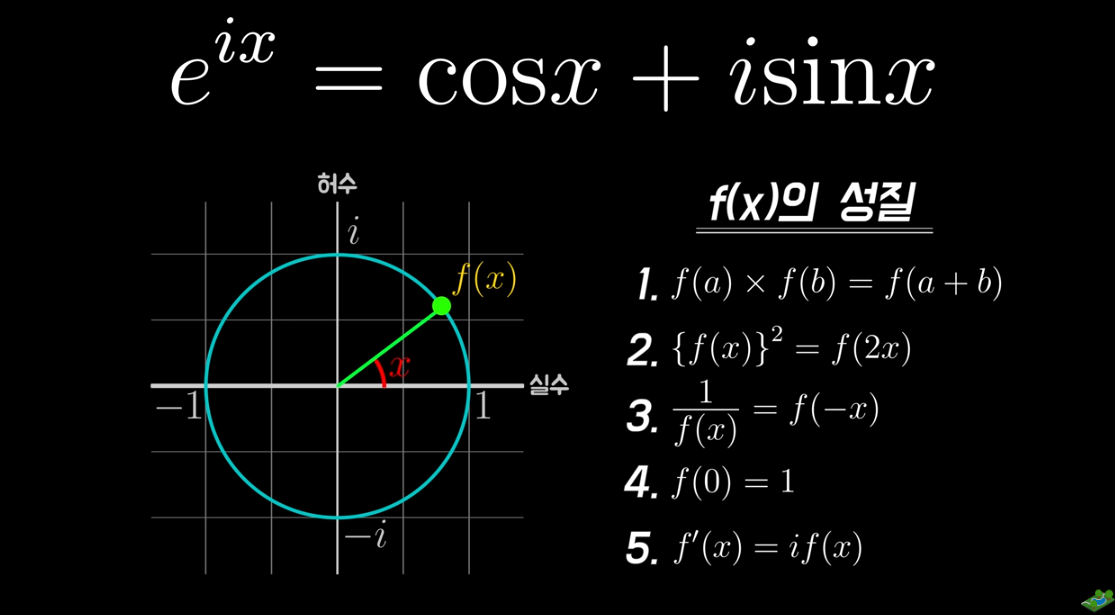


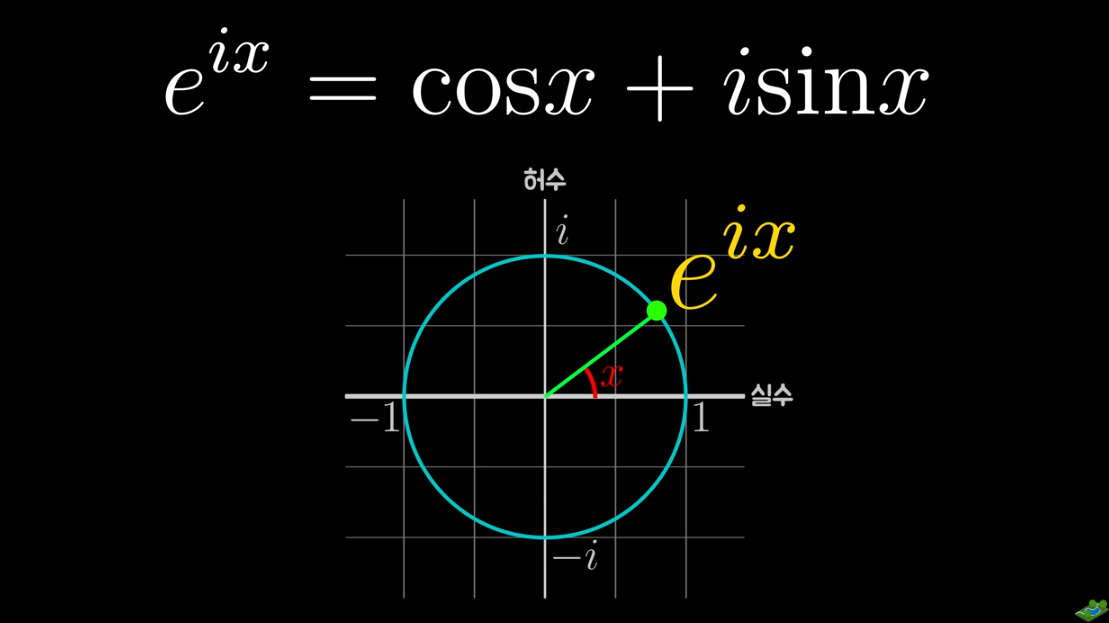

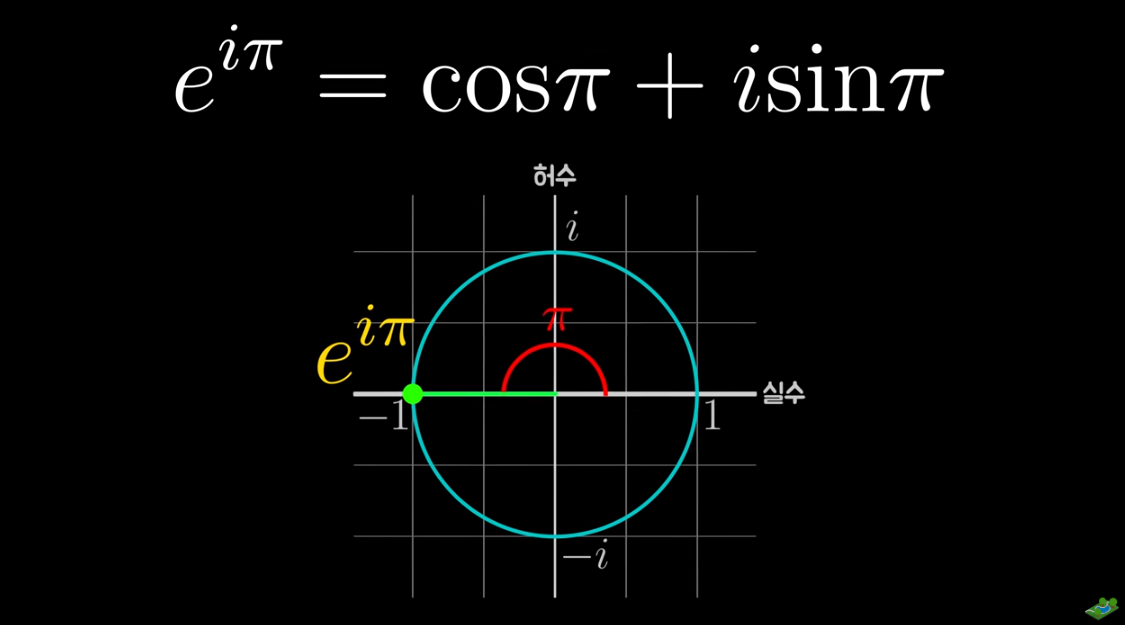
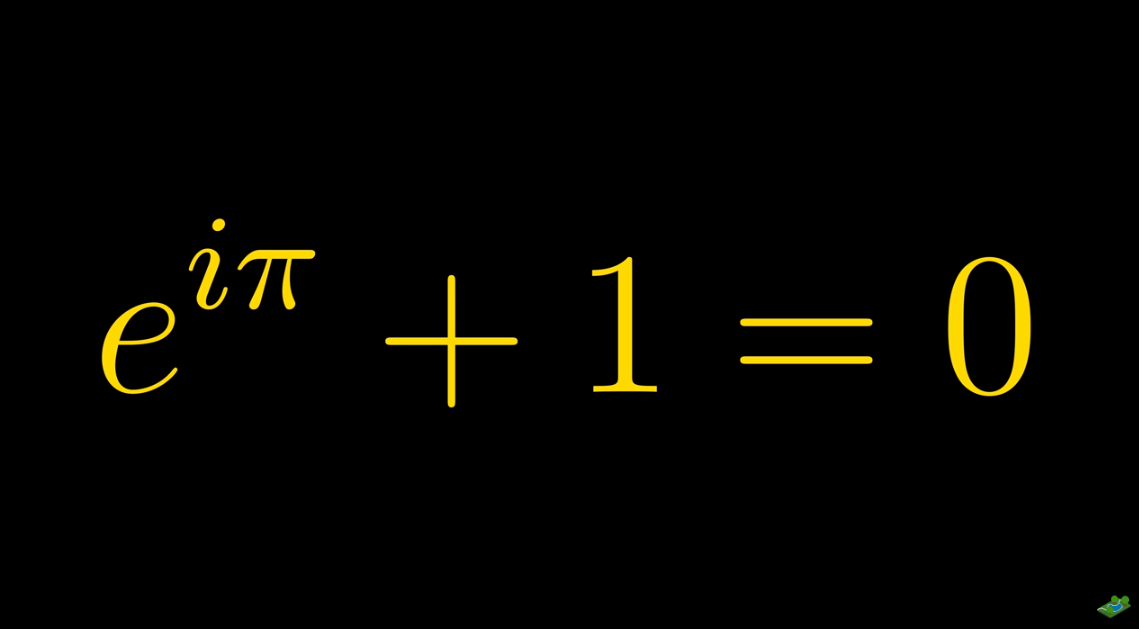
e의 iㅠ승은 복속 평면상에서 크기 1 편각 파이에 위치한 수, 그리고 그 위치에 있는 수는 -1입니다. 여기서 -1을 좌변으로 옮기면(e^iㅠ + 1 = 0) 이것이 바로 오일러 등식입니다. 오일러 수라고 불리는 자연상수 e은 미적분을 대표하는 수이고, 허수 i는 복소수를 대표하며, 원주율 𝝅는 기하학을 대표하고, 0과 1은 정보를 나타내는 최소 단위의 해당합니다. 이 중요하고 대표적인 숫자들이 단지 플러스(+)와 이퀄(=)만으로 연결되어 하나의 수식을 이룬다는 것은 마치 한 줄의 시가 수많은 상황과 감정을 함축하고 있듯이 이것은 자연의 신비를 가장 함축적으로 나타낸 한 줄의 시와 같이 느껴집니다.
'유익한 정보 > 박문호 박사' 카테고리의 다른 글
| 기억 강화를 위한 3가지 방법 (박문호 박사 3부) (3) | 2023.11.02 |
|---|---|
| 기억을 위한 고속도로는 느낌이다. (박문호 박사 2부) (0) | 2023.10.31 |
| 기억을 쉽게 하는 방법 (박문호 박사 1부) (0) | 2023.10.15 |
| 미분값이 패턴이다(패턴을 읽는것이 예측) (2) | 2023.10.05 |
| 박문호 박사의 패턴, 모순 그리고 집합론적 사고 (0) | 2023.08.11 |



